污水处理过程的多变量预测控制
在活性污泥法污水生化处理过程的控制研究中,可以作为受控变量和操作变量的有许多,如何进行输入输出变量配对,已经有一些经验法则,一般是与具体的工艺流程配置有关的。由于生化反应器内各子过程以及与二次沉降池之间的参数存在相互关联,采用单回路控制时系统间必然存在耦合现象。因此在设计控制系统时,更多地应该把生化反应过程的主要受控变量和操作变量作为一个整体考虑,即构造多变量控制系统。
本文以体现系统内部硝化及反硝化生化反应进展状况的2号生化反应器中的氨氮与硝酸氮浓度为被控对象,以溶解氧设定值(DO)及内循环流量为操作变量,采用活性污泥1号模型(AsM1)为控制器设计模型,设计了多变量预测控制算法。通过对ASM1模型的闭环控制仿真,结果表明多变量预测控制与传统的带解耦比例积分微分(PID)控制相比,在解耦和动态性能等方面具有更好的控制品质。
1 系统描述与控制方案设计
1.1 数学模型分析
典型的活性污泥法污水生化处理过程包括生化反应池和沉淀池,如图1所示。其中反应池分为5个池,沉淀池分为1O层。其数学模型由于其内部复杂的机理关系而非常复杂,最常用的数学模型是国际水质协会1986年推出的ASM1模型n],包含13种组分的变量,在流通中进行8个子反应过程。在每个生化反应池中,物料变化遵循物料平衡公式:
累积量 - 反应生成量 + 输入量 - 输出量(1)
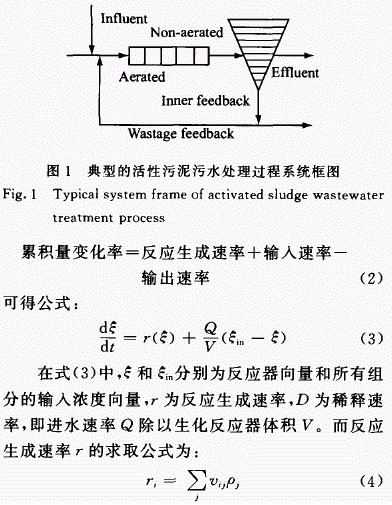

沉淀池的数学模型采用Takacs等。开发的二次指数沉淀速率模型模拟沉淀过程。由于在进行污水生化处理过程中的氮去除时,主要是控制生化反应中的硝化及反硝化反廊讲程,缺氧区的末端即2号反应器内的S N0和S NH 最为关键,因此可将该号反应器内的S N0和S NH 作为被控变量。
1.2 控制系统结构分析
对ASM1模型来说,污水处理的水质控制指标一般是S N0和S NH 若采用单回路PID控制,当内循环流量Q和溶解氧浓度DO变化时S N0和S NH 都将随之变化,两路输入与两路输出之间存在交叉耦合关系。
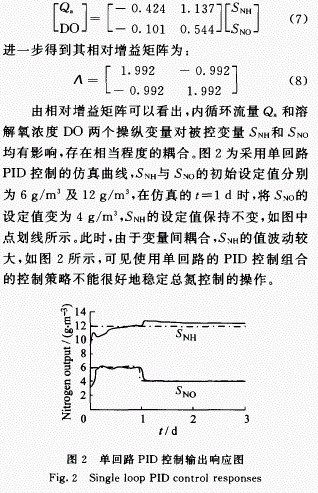
相对增益矩阵(RGA)[3]可用来分析多变量系统的变量间耦合关系,矩阵的各个元素反映了各输出变量受输入变量影响的程度。对ASM1模型在MATLAB/SIMULINK环境下进行仿真计算,得到内循环流量Q 和溶解氧浓度DO两个操纵变量与被控变量氨氮浓度S NH 和硝酸氮浓度S N0的稳态增益矩阵为:
2 控制系统设计及仿真
由以上分析可知,如果分别对S NH 和 S N0 进行单回路控制,不能解决 nS NH 和 S N0 之间存在的耦合问题。如果其中的一个变量出现波动,必将影响到另外一个变量的值,使之也出现波动,因而拟对这两个被控变量实施多变量预测控制方案。
首先采用稳态建模,在稳态下对Q 、DO施加阶跃输入,得到对象响应如图3所示,从而获得对象的预测模型。

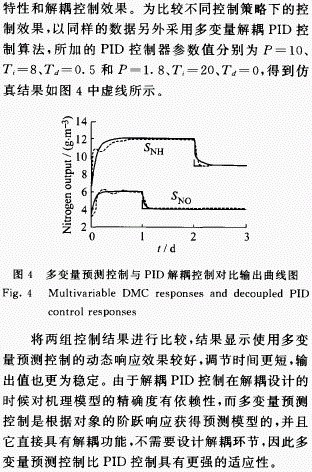
参考文献:
[1] Henze M,Grady Jr C P L,Gujer W,et al,Activated sludge model No.1[A].IAWPRC scientific and technical reports[c].London:IAWPRC,1987.
[2] Takacs I,Party G G,Nolasco D.A dynamic model of the clari-fication thickening process[J]Water Research,1991,25(10)1263-1271.
[3] 王桂增.高等过程控制[M].北京:清华大学出版社,2002.
[4] 舒迪前.预测控制系统及其应用[M]北京机械工业出版社,1996.

使用微信“扫一扫”功能添加“谷腾环保网”









